風險與報酬
日期:2007-02-08
常聽到網友們說,想找一種『低風險、高報酬』的投資標的,我都直接了當的告訴他們:這是不可能的。投資學第一課即是「風險與報酬之兌換」;也就是說報酬率高的投資商品一定得用風險來交換。
試想若有一個投資商品和定存一樣穩健保本又保息,而報酬率卻高於定存,那麼是不是會有一大堆的理性投資者會去買該商品呢?結果當然導致需求高於供給。根據市場法則,該商品價格往上推升,利潤自然就下降,報酬率自然就降下來;反過來說,若有一項風險的投資標的例如債券及股票,其所提供之報酬和定存一樣低,則將不會吸引投資者購買。所以該商品必需降低其價格,提供投資者夠多的利潤空間,才有客戶上門。
所以說,投資鐵律即為”高風險、高報酬”、 ”低風險、低報酬”,你不承擔風險是不可能得到好報酬的。
不承擔風險好嗎
要得到較高的報酬就必須付出風險的代價,因此許多人是選擇不要風險,寧可報酬低一些,才不會把辛苦賺來的錢給賠掉。這就是為什麼台灣有那麼多人投資人選擇放定存的原因了。但是要討論的是:
- 不承擔風險將失去了多少機會
- 承擔風險真有那麼可怕嗎
- 不承擔風險失去了多少機會
我們以台幣定存每年2.2%和投資組合每年8%來比較,現在投資100萬元
一年後:
2.2% 102.2萬
8% 108萬
雖然一年利息只差5.8萬,但是我們看看20年後會有什麼區別:
2.2% 155萬
8% 466萬
兩者差了三倍,不是三成喔!100萬一年定存會得到2.2萬利息,而風險性投資會平均得到8萬。很多人心想只差個幾萬塊,值得冒這風險嗎?可是數字告訴你,20年後會差到三倍之多,而且時間愈久差距愈大。
承擔風險有那麼可怕嗎
大家一談到風險就怕,以為會把心血賺的錢賠光光似的,其實風險是可管理及規劃的。風險有大有小,如果無法承擔大的風險,就選擇小一點的風險,投資學裡有一大半是在談風險管理,可見這有多重要。風險是可以隨自己所承擔的大小來做調整,就像你在調整電視機的音量一樣,要多大有多大,要多小有多小。這表示只要調整範圍在個人能承擔風險之內,相信很多人會願意承擔適當的風險,然後得到較高報酬的。
如何衡量風險
如果我們希望能調整風險大小,那麼我們必須先知道如何衡量風險。風險有許多種,諸如信用風險、波動風險等。但最難處理的是波動風險,就好像股價每天都在波動,是漲還是跌實在不知道。如下圖是MSCI世界指數圖,由這張圖我們只知道它一路往上爬,而且上下波動還不小,尤其是1999年那一段。可是這張圖無法帶給我們任何其他的分析。
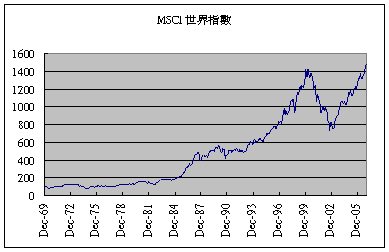
統計學家把這張圖的資料以每月為一期,計算當月報酬率,每年會得到12個月的報酬率。長期下來把這些報酬率做一張直方圖,觀察報酬率會呈現怎樣的分布呢?上下圖都是用同一組資料,卻有不同表現,一個是無法分析,另一個卻有規則可循。
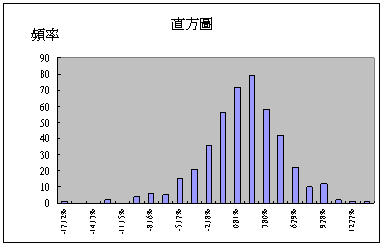
直方圖上呈現的是鐘型曲線告訴我們這是自然分配。這就好辦了,由統計學知道只要是自然分配就可以用平均值(μ)及標準差(σ)來分析。MSCI這組資料月報酬率平均值0.69%,月報酬率標準差4.1%。我們不要去管數學,只要知道其意義便可。自然分配代表報酬率會在平均值附近遊走,或稱為波動。至於波動大小由標準差決定,有68%的機會落於平均值正負一個標準差之間,95%的機會落於平均值正負兩個標準差之間。亦就是MSCI 世界指數每月報酬率:
68%的機會落於 -3.41%~4.8%之間
95%的機會落於 -7.51%~8.89%之間
衡量波動大小就是由標準差的值來決定,標準差愈大波動愈大,標準差愈小波動愈小。這直方圖的外緣像一個鐘一樣,標準差愈大這鐘型曲線愈胖,標準差愈小這鐘型曲線愈瘦。
年化報酬率可以用月報酬率直接乘以12求得0.69%*12= 8.28%
年化標準差可以用月標準差乘以12的開根號 4.1%*12^0.5 = 14.2%
如何調整風險大小
我們已經知道風險可以由標準差來衡量,但是已經知道投資標的的風險(標準差)又如何呢?如果風險性資產只佔整個資產的部份比例,而其他部分則投入無風險資產例如定存,那麼整個資產的風險自然降低了。而且如果風險性資產比例愈低,整體的風險就愈低。這道理大家應該都知道,但是混合起來確實數字會變成怎樣卻鮮為人知。下面為其公式
報酬率 = (定存比例 * 定存報酬率) + (風險資產比例 * 風險資產報酬率)
標準差 =風險資產比例 * 風險資產標準差
例如MSCI世界指數ETF,平均報酬為每年8.28%,標準差14.2%;而定存報酬為每年2.2%標準差0%,那麼混合這兩種投資標的,不同的比例會有什麼結果呢?
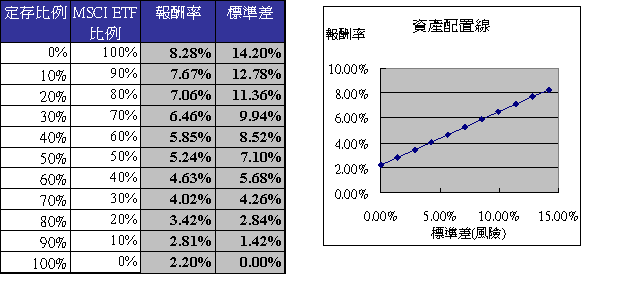
上表的第一行是完全100%投資MSCI ETF,所以報酬率8.28%和標準差14.2%完全和MSCI ETF一樣,愈往下看,定存比例就愈高,標準差就愈少,當然報酬率亦愈小。隨著定存比例往上升,我們可以看到標準差一路往下降,一直到零為止,那就是百分之百投資定存。這結果告訴我們什麼?只要調整定存比例,就可以調整風險大小。可想而知無風險資產在你的資產配置裡有多重要。
將上面表格中以標準差為橫軸(x),報酬率為縱軸(y),就可得到右上圖的資產配置線,橫軸標準差從0%到14.2%;縱軸報酬率從2.2%到8.28%。這條線的斜率代表每單位風險得到的報酬 (8.28%-2.2%)/14.2% = 0.43%。就是說每增加1%的風險(標準差)可換得0.43%的報酬率。斜率愈陡,代表承擔一單位風險得到的報酬愈高。這也告訴我們報酬是要用風險去換來的,用風險所換得的報酬稱之為”風險溢酬”。
例如MSCI World Index年化報酬率為8.33%,年化標準差為14.21%。我們如果投資100萬,可以70萬投資美金定存(4.8%),另30萬投資MSCI 世界指數的 ETF,這樣就可以將整組資產標準差等於14.21%*0.3 = 4.2%,當然整組報酬率也會降低4.8%*0.7 + 8.28%*0.3 = 5.844%。這組資產變成這樣:
年報酬率:5.844%
年標準差:4.2%
這組資產未來會如何變化
其實一般投資人對統計及標準差是陌生的,經過計算得到了一組數字:年報酬 5.84%及4.2%標準差的風險,但怎麼知道是不是我能承擔的?尤其是什麼時候該買,什麼時候該賣?怎麼都沒提到呢?買賣股票及基金不都是該這樣嗎?
其實那些都是錯的,只要持有該資產放著不管就可以了。因為你已經預知該資產可能變化情形,年報酬率平均值5.84%已經說明會淨值會以平均5.84%的力道往上爬升,只是不會剛好是5.84%而已,但是大部分時間(68%機會)會落於1.64%~10.04%。如果都放著不管,一年就會有這種變化,幾年下來會變成怎樣呢?如果可以預知這組資產淨值未來可能變化的情形,投資者便可自行判斷這組資產是否適合自己了。我用的方法是直接去模擬未來,取用亂數表來產生報酬率,代表每年報酬率是會隨著平均值變化,但如何變化是沒規則的,我提供了一個Excel檔來模擬未來十年可能的變化?
下載試算表
我用亂數表產生100組,每組有十年的報酬率,其報酬率及標準差符合所設定的參數B1 (報酬率)及B2(標準差),起始淨值每次都由100開始,每年根據報酬率重新計算淨值,下圖是100組的淨值路徑,你可以看到第十年大部分落在150~200之間,只有少部分稀稀落落在外面。
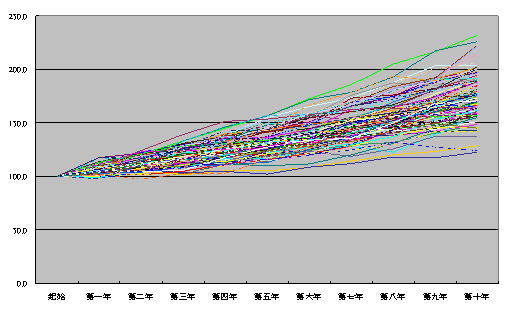
把這些資料整理一下,把每年100組的淨值求平均值及標準差,就會得到下一張圖表,淡青色線條夾角部份是一個標準差(68%)波動的範圍,粉紅色線條夾角範圍為兩個標準差(95%),你可以感受一下這波動會是多大。任何時刻你都可以改變B1及B2儲存格的值,再看看未來十年走勢如何。標準差值愈小,你可以觀察到波動的範圍就小了,粉紅色及淡青色夾角就愈小。
下圖是年報酬率:5.84% 年標準差:4.2%的結果,你可以看到雖然頭一兩年還是有可能為負值,但往上的方向是對的。如果這讓你不舒服,再調高定存比例吧!縮小標準差,會讓你睡的安穩些,但同樣的你得損失報酬。
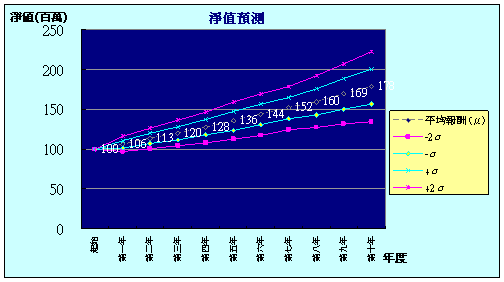
提高單位風險之報酬率
既然報酬是要承擔風險去換得,當然承擔相同風險所得到的報酬愈高愈好,這就是資產配置的課題。由『如何調整風險大小』這節裡的資產配置線為例,要讓資產配置線變陡,就必須將基金的標準差(14.2%)維持不變,而報酬率要提高(>8.28%) 才有可能,或者是報酬率維持不變,降低風險。將兩種以上的不同屬性基金依不同比例混在一起,是會降低風險的。然而如何將兩個或多個基金混在一起而得到最佳報酬/風險的比值,稱之為”資產配置”。
對這題目有興趣讀者請參考仿間投資學或我網站資料






