理財基本功 用Excel算複利
日期:2014-07-31
在電腦為普及之前,有關投資理財的計算,都只能依賴算盤。自從個人電腦開始流行,取而代之就是電腦及雲端試算,而微軟的Excel堪稱是目前最容易取得的工具之一,學校許多科系也會教授Office課程,足見Excel的重要性。一位稱職的投資者,除了應有的理財知識之外,若能將Excel學好,會是如虎添翼,把理財功力往上推進另一個境界。
基礎複利公式
複利是投資理財的基礎,幾乎所有的投資理論都會用到,不能不知道,公式如下:
期末淨值=期初投入×(1+投資報酬率)期數
期末淨值就是期初投資,經過一定的期數之後,以複利成長的金額。因為銀行的年利率就是年化投資報酬率,銀行期末存款淨值使用另一個名稱,期末本利和。
上述複利公式,期數並沒有時間限定,可以是一年一期或者是一個月一期,也可以是一季一期。只是報酬率的期間必須和期數一致。例如每年一期,就得使用年報酬率,若是每月一期,就得使用月報酬率,而月報酬率等於年報酬率除上12,依此類推。
上述複利公式是指數函數,得換成Excel可以使用的方式才行。若要計算期末淨值,只要在工作表上任何一個儲存格內輸入以下公式就可以了。
=期初投入*(1+投資報酬率)^期數
“*”就是乘號,“^”就是次方的意思,輸入的方式是按著SHIFT鍵不放、再按6。
例如James拿出10萬元,投資銀行定存,年利率1.5%,5年後可以拿回多少錢?
只要在任何儲存格輸入=100000*(1+1.5%)^5,就會顯示答案107,728。要特別注意的是逗點在Excel中有特別意義,其中數字不可以加千分位。而且可以直接輸入百分比,不用自行將1.5%換算成0.015。
再舉一個例子,Michelle同樣也拿出10萬元,但是投資股票基金,若平均投資報酬率為12%,5年後基金淨值會是多少?
只要在儲存格中輸入=100000*(1+12%)^5,就會得到答案176,234。
報酬率就是成長率
其實,報酬率就是成長率,所以也可以用在估算現值經過通貨膨漲後的金額。例如現在的小孩上大學,每年所需費用30萬元,若小孩目前只有2歲,16年後才會上大學,預估那時候的學費要準備多少?
預估未來的平均通貨膨漲率每年為2.0%,第16年的費用經通膨調整為41萬1,836元,公式如下【=300000*(1+2%)^16】。16年以後需要41萬1,836元,那麼現在就得要準備多少錢,才足夠應付呢?這得要看投資報酬率是多少了,如果投資較保守的債券基金,報酬率估計每年可達5.0%。只要將複利公式稍微改變一下,就可以在已知期末需求金額、投資報酬率、期數的條件下,求得期初需要投入多少,也就是現值的金額。
期初投入=期末淨值/(1+投資報酬率)期數
所以16年後的41萬1,836元,若以5.0%投資報酬率估算,只要準備18萬8,667元就足夠,Excel公式如下【=411836/(1+5%)^16】。
製作實用的Excel試算表
上述公式只有上大學一年級的學費,如果大學加上研究所一共需要6年,每年的費用經過通膨調整後都不一樣,且現值也會不一樣。如果要一個個公式分別輸入也未嘗不可,但是每當條件改變時,公式就得一一跟著調整才行,麻煩又容易出錯。一個好用的試算表,必須滿足使用者可以任意更換試算條件。例如當通貨膨脹率、或者投資報酬率改變時,需要總現值是多少。本篇教導讀者如何製作一個好用的試算表。
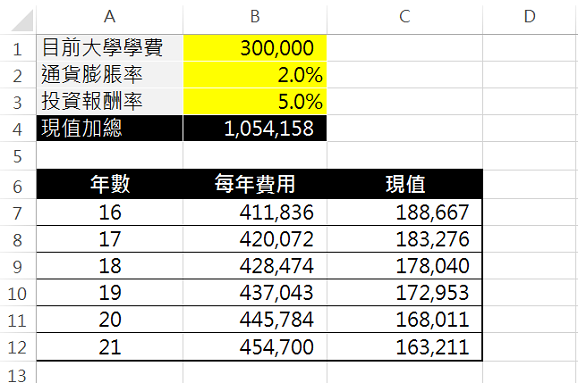
下圖是製作好的試算表,可點擊下面的Excel圖示下載:
黃色的儲存格為可調整參數,而B4的儲存格就是試算後結果,就是小孩未來6年的學費,現在總共得準備多少金額。A7:C12是試算的明細,年數欄位是學費幾年後會用到,每年費用欄位是經過通膨調整後的學費,現值的欄位是每年費用以投資報酬率折現後的金額。儲存格B4的公式,就是將每一年的現值(C7:C12)全部加起來,也就是最後的答案。
如何製作試算表
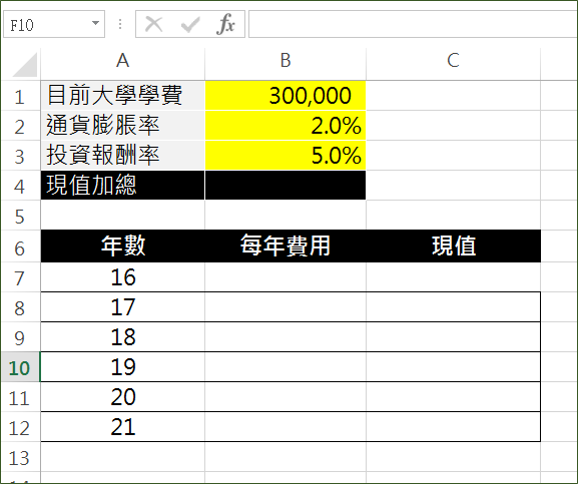
- 首先輸入下圖中的文字及參數(如下圖),這些都只是文字及數字,沒有任何公式。
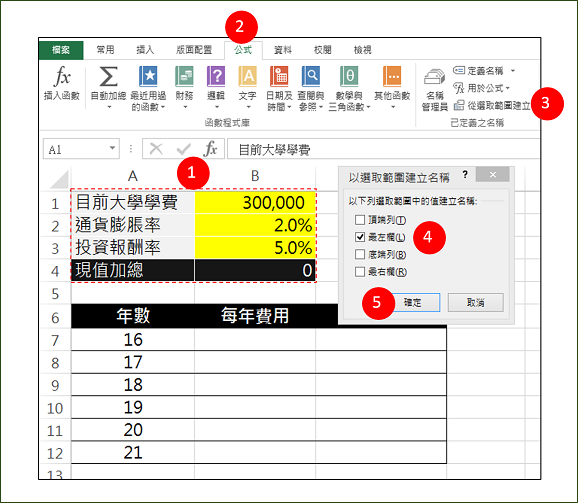
- 接著先定義參數的名稱,先用滑鼠選取A1:B4的範圍(下圖 1),點選“公式”頁面(下圖 2),再點選“從選取範圍建立”(下圖 3),這時就會跳出“以選取範圍建立名稱”小視窗,勾選“最左欄”(下圖4)。按確認鍵(下圖 5)結束。這時B1儲存格名稱已經重新被定義成目前大學學費,B2重新定義為通貨膨脹率,依此類推。
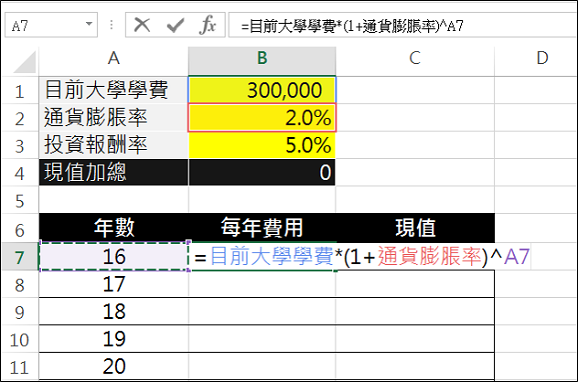
- 輸入B7儲存格公式 =目前大學學費*(1+通貨膨脹率)^A7,完成後B7會顯示計算結果。
- 輸入C7儲存格公式,=B7/(1+投資報酬率)^A7,完成後C7應該會顯示計算結果。
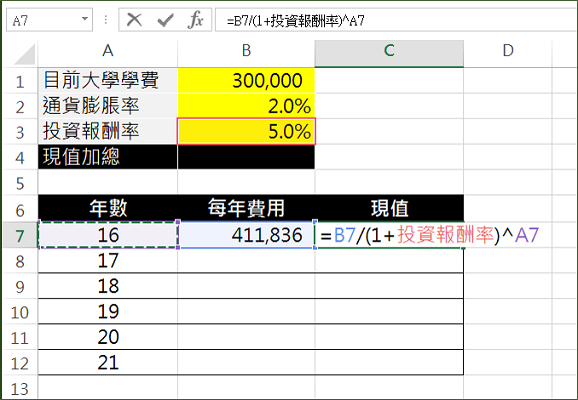
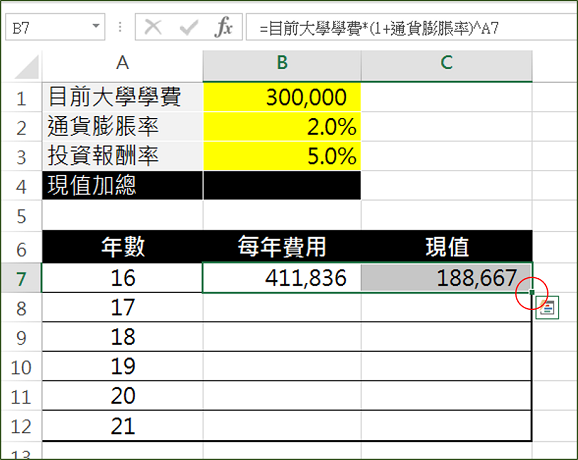
- 接著用滑鼠選擇B7:C7的範圍,然後將滑鼠對準C7儲存個的右下角的小點(下圖的紅圈),當滑鼠出現”+”號時,快速點擊兩下,就會將B7:C7這一列的公式,複製到其他列上(B8:C12)。
- 最後輸入B4儲存格的公式 =SUM(C7:C12) ,將所有現值加總就大功告成了。
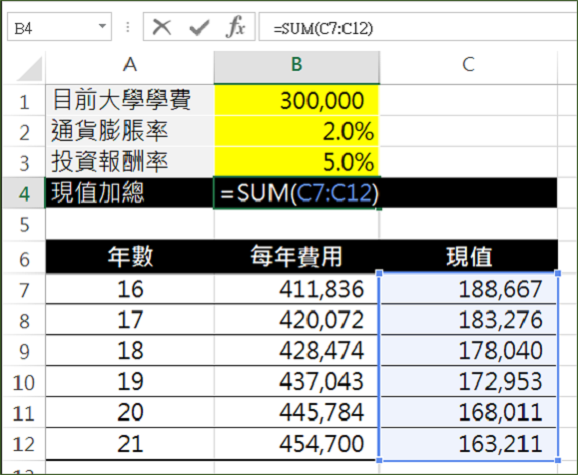
有了這份試算表,黃色區域的儲存格都可以任意更改,答案立即顯示於B4儲存格中,不只是快速又方便,而且計算明細也都看得清清楚楚,是個值得學習的好方法喔。







