資產配置
日期:2008-04-06
兩組資產配置會減少波動
兩組資產配在一起時,會讓整體波動減少,而減少的程度和兩組資產的相關係數有關。
- 如果兩組資產相關係數為"+1"時,代表兩組資產絕對正相關,當一組資產漲的時候另一組資產一定(100%)會漲,反之亦然。這時波動不會減低亦不會增加。例如台灣的兩支股票型基金,往往相關係數相當接近一。
- 如果兩組資產相關係數為"0"時,代表兩組資產無任何相關性,就是說一組資產漲的時候另一組資產可能漲亦可能跌,不知道而且不一定,就因為這樣某些時候表現會相對抵銷,所以說波動會減低。例如一支股票型基金及另一支債券型基金,因為兩者基金型態不一樣,所以相關係數接近零,波動會抵消。
- 如果兩組資產相關係數為"-1"時,代表兩組資產絕對負相關,當一組資產漲的時候另一組資產一定(100%)會跌,反之亦然,因為兩者一定互補,所以可以配出一套報酬高及零風險的配置出來。不容易找到相關系數為"-1"的兩組基金,如果有就發財了。
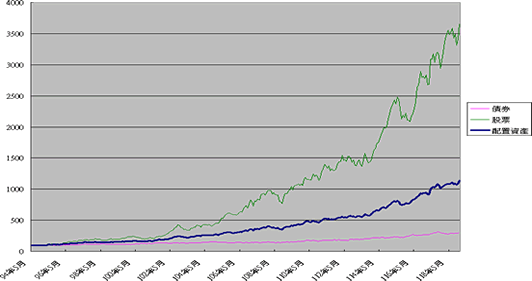
由上面所述相關系數為 -1~+1,好的資產配置應該儘可能選擇相關系數為負或者是零。下圖示以債券(粉紅色)和股票(綠色)配置後(藍色)的結果(相關系數 0.2),您可以看得到配置後(藍色)的波動程度是比股票還好,當然報酬率亦會相對於股票減低。
資產配置模擬
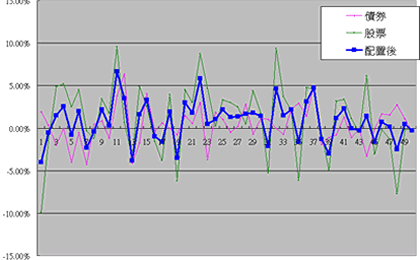
每一檔股票或者基金,從長期的角度來看都可以用兩個參數來表示,一個是平均報酬率另一個是標準差(風險),那麼當我們知道自己擁有的基金及股票的參數時,可以預測持有10年或20年會有什麼結果嗎?我們可以利用微軟的Excel幫我們模擬,下圖綠色的部份是模擬一般股票型基金35年的結果,粉紅色則是債券基金同時間之結果,藍色部份則是股票基金及債券基金各半,並假設兩者相關系數為零之混合結果。我們可以發現混合結果波動是那麼的小,而結果比債券基金大三倍左右。因為是利用Excel亂數表為基礎模擬,你可以得到以下結論『不論如何波動,是一路往上爬』。
你可以按下圖直接開啟或下載excel的檔案來觀看不同次模擬結果,該檔案有兩個工作表一個是"指數模擬"圖表另一個是"模擬資料"表,你可以在任何一個工作表上按F9就會重新模擬一次,你可以看到結果都相去不遠。在"模擬資料"工作表上的黃色儲存格你可以重新定義你自己個股票基金及債券基金之報酬率及標準差以及投資比例,按F9就會重新模擬一次。
用Excel做有趣的模擬實驗
許多人看了資產配置模擬後都有一個疑問,為什麼用Excel的亂數表可以模擬股票或者債券市場行為,這樣模擬可信度有多少?為了回答這些問題我用了兩個有趣的例子來證明模擬是非常方便及有用的,一個是用丟石頭的方式求圓周率π,另一個是模擬五十人的生日看有多少人同月同日生。
丟石頭求圓周率π
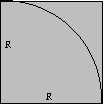
當我在學校時候,一位統計學教授敘述了一個故事,在很久以前有一位數學家利用丟石頭的方式求得了圓周率(π=3.14..),方法是這樣的:那位數學家在地上畫了一個正方形,再利用繩子畫一個1/4圓,然後數學家在距離正方形大約五公尺的地方,背對著正方形投下一萬個石頭,然後計算石頭落在扇型面積內的數量以及正方形內石頭數量的比值,圓周率π就是這比值的四倍,求出答案後結果卻是出乎意料的準確。
以前只是聽聽覺得好奇但無法快速實驗,時過25年現在有了Excel便興起做實驗的慾望,做完這實驗當下還覺得頗有成就感的,提出來與各位分享。如果有人知道這位古數學家的名子,請告訴我好添增這篇文章的可看性。
正方形面積 = R*R
扇形面積= (π* R*R)/4
扇形面積 / 正方形面積 =π/ 4
π= (扇形面積 / 正方形面積) * 4
就是說π= 扇形面積及正方形面積比值的4倍。
而石頭落在扇形面積的數量和落在正方形面積數量之比值,應該等於扇形面積及正方形面積之比值,所以
π= (扇形面積石頭的數量/正方形面積石頭數量) * 4
Excel如何模擬丟石頭
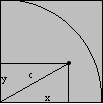
我們可以使用兩個Excel儲存格代表座標x, y,儲存格輸入亂數產生器函數=rand(),因為rand()會產生0~1的實數,所以 x, y <= 1而且正方形面積為1*1= 1,圓的半徑為1。每一(x, y)組合相當於一顆石頭的位置,我們可以利由畢氏定理判別x, y組合的斜邊 c是否大於圓的半徑"1"來判定這石頭是在扇型面積內或外。根據這原則我們複製10,000對(x,y)儲存格就好像丟10,000顆石頭。
![]()
如果 c <= 1,扇型面積內
如果 c > 1,扇型面積外
另一個有趣模擬-相同生日
有一次拜讀林基源先生的"決策與人生"這本書(遠流出版),裡頭提及在一個50人的派對裡,有一對以上的人同月同日生的機率是97%,雖然書裡頭的証明無誤,心中不免存疑,當下立即拿起Excel模擬一下,結果的確如書中所提,只好趕快了解如何證明。
Excel模擬50人的生日(月/日)
如果要去隨機找出真實50個人的生日,尤其是還得一一比對他們之中是否有同月同日生,實在是需要費點功夫。尤其是如果這五十人剛好沒人是同月同日生時,到底是理論錯還是這組樣本恰巧是那3%裡的其中一組,所以要驗證這理論只有一組樣本還不夠,至少還得找100組人當樣本(每組50人),檢查看看100組樣本裡是否有97組都有一對以上的人有相同生日,哇~~~這工程還不簡單呢。
還好有了Excel的亂數產生器幫我們省了許多麻煩,只要用50個儲存格代表50個人的生日,每一儲存格放公式=randbetween(1, 365)會產生1到365的亂數,使用亂數可以模擬隨機抓到一個人然後問他的生日,"1"就代表一月一日"2"代表一月二日,依此類推"365"代表十二月三十一日。再由Excel自動檢查這50個儲存格是否有重複號碼。為方便起見,我已輸入檢查公式,粉紅色儲存格表示有相同生日的人,你可以很清楚辨認是否有相同生日的人。
您可以按"F9"鍵這時50個儲存格的亂數產生器會更換一組新值,代表另外一組50人的生日樣本,按"F9"鍵100次就代表找了100組人,每按"F9"鍵一次就檢查看是否有人同月同日生,你會發現真的如書上所說只有三組人都沒有人有相同生日。
如果你真做了實驗,會發現並不是那麼準確的"三次"槓龜,可能是兩次或四次,這是機率問題,如果你按1000次應該會更接近30次(3%)槓龜,這是因為樣本數愈多會愈準確。
注:因為randbetween(1, 365)這函數要Excel2003以上才有,為了普遍性所以用改用=ROUND(RAND()*365,0)這函數替代