EXCEL財務函數-PRICE
日期:2009-03-08
一般財務教科書以及本網站其他有關債券文章,都比較偏重觀念性的介紹。對於如何計算債券的價格及殖利率, 一般也都予以簡化,對於實際應用幫助不大。然而Excel提供了許多有關實務上會用到的債券的計算函數,使用起來非常方便。這篇只主要探討Excel PRICE這函數,不只告訴你如何使用PRICE函數,也將剖析公式的由來,讓讀者知其然也知其所以然。提醒讀者要使用PRICE函數,必須將工具/增益集的『分析工具箱』打勾才可。
百元報價方式
債券的買賣金額通常是很大,可是債券的報價卻是以100元為單位,意思是每100元票面金額的債券價格。這樣有何好處呢?其實這100元所代表的是百分比的意思,例如當債券價格是103.619時,實際交割金額是票面金額的103.619%。例如債券票面金額為100萬,那麼交割金額就是1,000,000*103.619% = 1,036,190元。
以百元為報價基礎的優點是:不論哪一個債券,也不用知道票面金額多寡,一看就可以知道目前殖利率相對於票面利率的狀況。當債券價格大於100時,殖利率一定低於票面利率。相反的,當債券價格低於100時,殖利率一定比票面利率還要高。當然,債券價格等於100時,殖利率就一定等於票面利率。
債券價格(Price)和殖利率(Yield)
下圖是一債券從發行至到期日的現金流量圖,白色長條圖發生在交割日之前是已經支付過的票息,對債券價格毫無意義。黃色長條圖是未來將會收到之票息,綠色長條圖是代表到期日會收到之票面金額。債券的價格是將該債券交割日後所產生的票息(黃色)及票面金額(綠色)以殖利率(Yield)折現之總和。因為票息和票面金額是固定的,然而殖利率是隨著市場波動而變,所以當殖利率變動時,債券價格就會跟著動。反之,當債券價格為已知時,也可以反推債券的殖利率是多少。
雖然買賣是以價格為基礎,但是投資者對殖利率是比較有感覺的,所以債券價格習慣以殖利率來報價。也因為一個殖利率就隱含著一個債券價格,所以債券報價都是(價格/殖利率)成雙成對出現的。
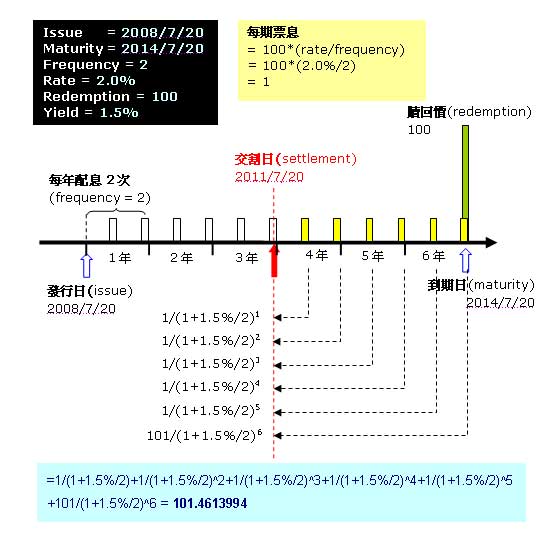
以上圖為例,一個2008/7/20日發行的債券,票面利率2.0%、每半年付息一次,2014/7/20到期還本。假若投資者要求的殖利率(Yield)是1.5%,那麼該債券的價格就是將未來支付的票息及本金以殖利率折現的總和。
假若購買交割日為2011年7月20日,“剛好”和付息日是同一天7月20日,未來每半年支付的1元票息,都剛好是一整期(半年),所以折現方式就很簡單了:
- 第1期:1/(1+1.5%/2)1
- 第2期:1/(1+1.5%/2)2
- 第3期:1/(1+1.5%/2)3
- 第4期:1/(1+1.5%/2)4
- 第5期:1/(1+1.5%/2)5
- 第6期:101/(1+1.5%/2)6
最後一期(第6期)折現金額為101,是將票息1元加上票面金額100元的結果。所以債券價格等於:
Price = 1/(1+1.5%/2)1+1/(1+1.5%/2)2+1/(1+1.5%/2)3+1/(1+1.5%/2)4+1/(1+1.5%/2)5+101/(1+1.5%/2)6
以Excel公式表示
=1/(1+1.5%/2)+1/(1+1.5%/2)^2+1/(1+1.5%/2)^3+1/(1+1.5%/2)^4+1/(1+1.5%/2)^5+101/(1+1.5%/2)^6
=101.4613994
Excel PRICE函數
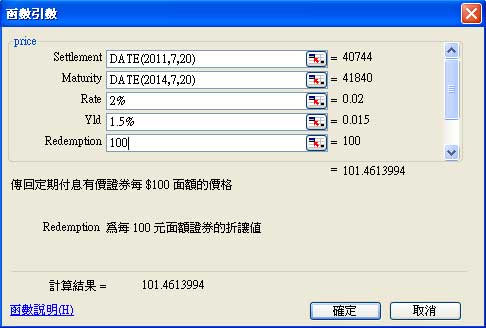
其實不用那麼麻煩,大費周章的用折現公式一一加總,Excel提供一個非常簡便的財務函數PRICE,主要就是針對債券價格計算而來。只要依下圖分別填入交割日(Settlement)、到期日(Maturity)、票面利率(Rate)、殖利率(Yld)、票面金額(Redemption),以及配息次數(Frequency)。一個公式都不用寫,馬上就會得到答案,而且跟個別票息折現方法的結果是相同的:
=price(DATE(2011,7,20),DATE(2014,7,20),2%,1.5%,100,2)
=101.4613994
使用PRICE函數必須將增益集的『分析工具箱』打勾,否則會出現 #NAME? 錯誤。方法是:
1) 工具/增益集
2) 『分析工具箱』打勾
3) 按確定
請注意:日期需要用Date(年,月,日)格式輸入才可
付息期間交割之債券價格
前面所述之債券價格計算都是假設交割日和付息日是同一天,所以折現方式很簡單。但是若債券之買賣(交割日)落於兩個付息日期間(如下圖所示),這債券價格又如何計算呢?
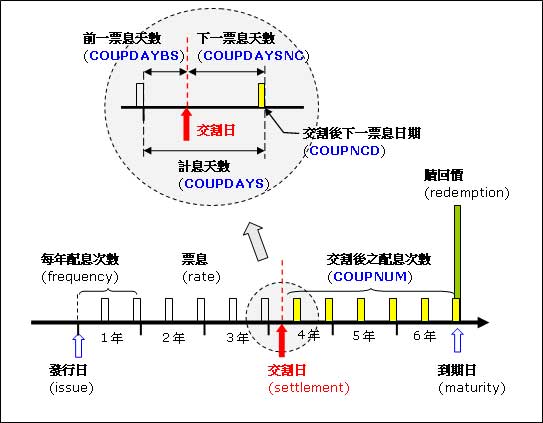
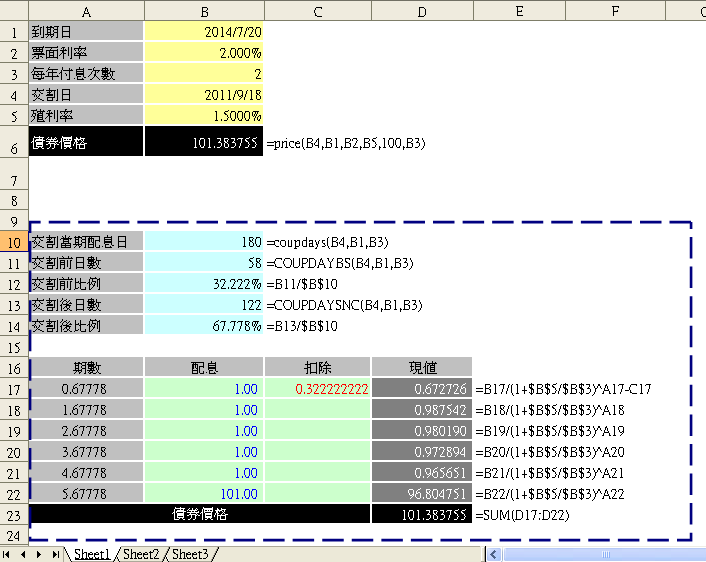
第一個面臨的問題是未來現金流量如何折現呢?已經不再是期數的整數倍了。還好數學還有分數指數可以用,利用同樣的折現方式,只是期數的部份改為分數而已。既然是分數,只要將交割日佔前後期的比例先算出來就可以了。下圖的Excel以交割日2011/9/18日為例,做了詳細說明。A1到B6儲存格的部份是直接用PRICE函數計算的,只要將債券的參數輸入(B1~B5黃色儲存格),B6立即會算出該債券價格。將交割日(B4儲存格)填入2011/9/18日,B6馬上算出債券價格是101.383755元,確實是一個超好用的函數。
Excel檔案下載
A10到D23範圍的儲存格,都只是為了說明PRICE函數是如何計算的明細表(藍色虛線框起來部份)。重點在交割日後第一期,因為不足一期,必須算出佔整期的比例,才有辦法將第1期的票息折現,第2期以後只要將前一期加一即可。計算方式是先算出交割日該期的計息日數有幾天(儲存格B10),然後求出交割日到下一付息日的日數(儲存格B13),兩者相除就可求出比例(儲存格B14)。由B14結果顯示,交割後到第一付息日為0.67778期,所以第1期的票息折現公式=1/(1+1.5%/2)0.67778,第2期=1/(1+1.5%/2)1.67778依此類推。
除了用分數指數折現之外,因為交割日在兩期付息日之間,交割日前的利息必須在下一付息日才會支付,這一部分是不屬於債券購買者的,必須扣除掉才是債券的真正價格。所以扣除部分是當期票息1元(儲存格B17)乘上交割日到前期付息日所佔比例(儲存格B12),也就是儲存格C17所示的0.322222222元,於頭一期(D17)先行扣除掉。儲存格D23是D17到D22每期現值加總,就是債券價格。可以看出D23得到的數字,和B6用PRICE函數所算出的一模一樣。
其實這例子也可以用下列方程式表示,算出的結果也是一樣的。
Price = 1/(1+1.5%/2)0.67778+1/(1+1.5%/2)1.67778+1/(1+1.5%/2)2.67778+1/(1+1.5%/2)3.67778+1/(1+1.5%/2)4.67778+101/(1+1.5%/2)5.67778-1*(58/180)
用Excel公式表示上式:
=1/(1+1.5%/2)^0.67778+1/(1+1.5%/2)^1.67778+1/(1+1.5%/2)^2.67778+1/(1+1.5%/2)^3.67778+1/(1+1.5%/2)^4.67778+101/(1+1.5%/2)^5.67778-1*(58/180)
= 101.3837533
實務演練
學會了如何使用Excel PRICE函數,讀者可以看看台灣的債券報價,直接用PRICE函數算算看了。債券報價網站: