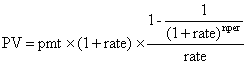年金Annuity-理論篇
日期:2009-06-15
只要是每一固定時間都有一筆收入或支出的財務型態都稱為『年金』。在生活周遭中有許多數不清的年金例子,諸如房屋貸款、分期付款、年金保險、國民年金等都是屬於年金的一種。這裡除了學到年金的概念之外,更將學會使用Excel解決各式各樣複雜的年金計算。
年金的型態
年金到底長的像什麼樣子呢?從現金流量圖最能看清楚年金的樣貌,還很輕易的分辨出年金的種類呢!。
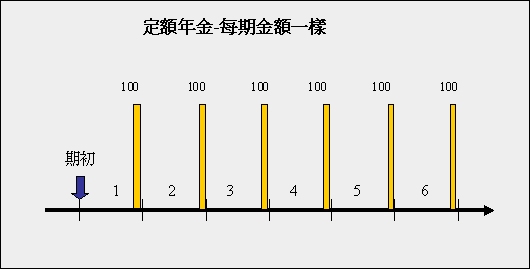
定額年金
定額年金就是每期的現金流量都是同等金額,如下圖所示現金流量圖看起來是平的。例如分期付款、房屋貸款以及銀行的零存整付定期存款,都屬於定額年金的範疇。
變額年金
變額年金顧名思義就是每期的金額都不一樣。變額年金基本上分兩種:一種是每期以前期一定比例成長,另一種是每期金額都不一樣,而且沒有規律。
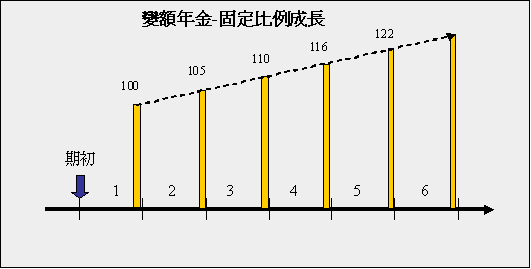
固定比例成長之變額年金
固定比例成長之變額年金是:每期的現金流量會以一定比例(g)成長,也就是當期的現金流量是前一期的(1+g)倍。例如保險公司為了解決通獲膨脹的問題,設計了一個年金保險,每年(期)所領的年金是去年的(1+2%)倍,這2%就是保險公司認為的通貨膨脹率。或者因應薪資收入會隨者時間成長,銀行也可以提出另一種貸款的還款方式:每期的還款金額是前期的(1+g)倍,這樣借款者就可在自己能力之下,較快的還清貸款。
非固定比例成長之變額年金
非固定比例成長之變額年金是:每期的現金流量並沒有一定規則可循,不過『通常』會圍繞於隱含的平均線上下波動。最典型的例子是與投資商品連動之年金保險。為求取更大的報酬,某些年金保險將一部份保險金額和投資商品連動,這樣的年金給付就每年不是很確定,得依投資狀況而定了。因為只有一小部分拿去投資,所以基本上每年給付金額會在一固定金額上下波動。波動的程度則和投資比例有關。
期初與期末
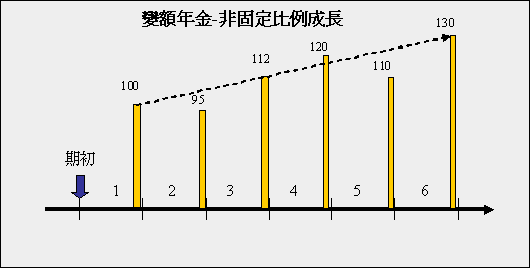
不論何種型態的年金,每期的現金流量還有『期初』以及『期末』之分。以下圖的定額年金為例,分上下兩個現金流量,同樣都是6期,每期金額都是100元,但是上面的現金流量都發生於每期之期末,下面的現金流量都發生於每期之期初。
舉個例子來說,Peter計畫於每年的『年初』存入1萬元,期間為10年,年利率5%,求10年底時的終值。因為都在年初存錢,所以這就是一個期初的年金。另外一例是,Rose跟銀行貸了一筆款項,期間為2年,年利率5%,約定每月『月底』償還本息2萬元,求貸款金額。這個例子每月為一期,總共24期,每月償還的本息均發生於期末(月底),所以這是一個期末的年金。
如何計算年金現值及終值
關於年金投資者最想知道的是年金的終值或現值。例如每月存一萬元款的零存整付定期存額,一年到期後可領回多少錢。又如每月繳房貸2萬元,以年利率3%繳了20年,到底值現在多少錢?
這些年金的現值與終值都有公式可以計算,不過要了解那些公式可是需要點數學功力,尤其是固定比例成長之變額年金更是複雜難懂,更別談非固定比例之變額年金沒有公式可算。怪老子並不想探討這種老式的學習方式,而是提供一套通用的Excel財務模型,計算所有年金的現值與未來值,讓所有型態的年金都可適用。
單筆之現值與終值
年金其實就是有多筆現金流量的意思,最簡單的計算方式是:將每一期的現金流量當做單筆來計算現值或終值,然後加總每一筆的現值或終值。設單筆之金額為PV,以每期利率rate經過n期後,單筆終值公式:
FV = PV*(1+rate)n -------公式(1)
例如單筆112元,以利率5%經過3期後,未來值 FV =112*(1+5%)3,以Excel公式表示:=112*(1+5%)^3 = 129.65
若未來值FV為已知,根據公式(1)可以反推單筆的現值公式:
PV = FV/(1+rate)n -------公式(2)
所有型態的年金現值及終值,都只需要用到這兩個公式。
Excel計算終值與現值
不用去管年金的公式,只要知道計算原理,便可以很輕鬆、而且非常清楚的的利用Excel將年金計算出來。首先請下載Excel範例檔案。這Excel檔案有兩張工作表:
- 等比年金試算
- 非等比變額年金
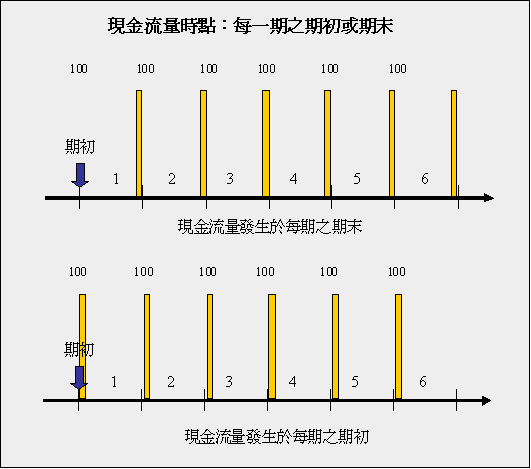
兩個工作表大致一樣,B欄(儲存格13以下)放的是每期之現金流量,C、D兩欄是『終值』的計算,C欄是期末,D欄是期初。E、F兩欄是『現值』的計算,E欄是期末,F欄是期初。
年金之終值
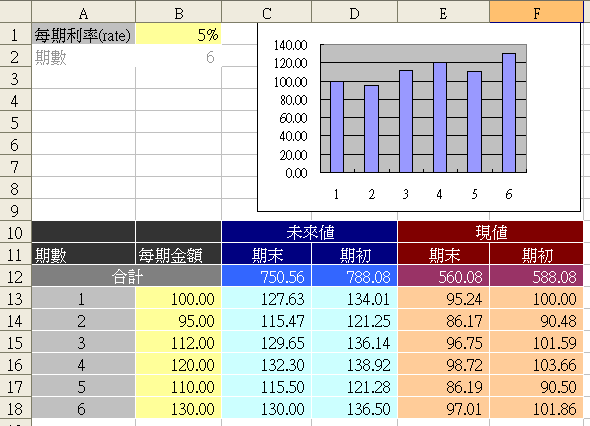
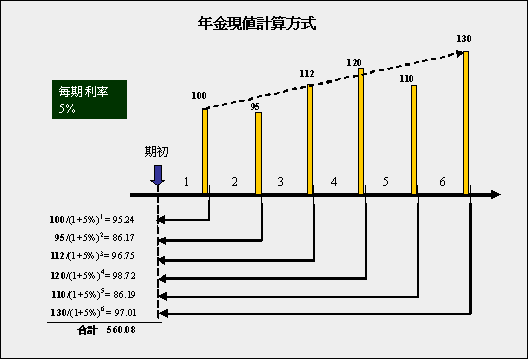
下圖是非固定式變額年金,每期金額都不一樣,所以說只要分別將每期金額都當做一筆單筆來計算終值,然後再全部加總就好了。這種方式最適合Excel的計算了,不需要去了解那些繁複的公式,只要加減乘除就可以了。
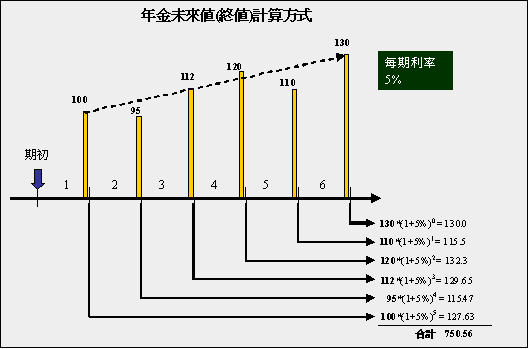
上圖的現金流量表示於儲存格B13~B18,因為現金流量是都發生於期末,所以只要看C欄就可以了。C13~C18就是計算B13~B18每一『單筆』的未來值,用的都只有公式(1)。例如C13是計算B13的未來值、C14是計算B14的未來值,依此類推。儲存格C12就是年金的終值:也就是C13~C18的加總。
若現金流量是都發生於期初,如果要看終值得計算,只要看D欄就好了。D欄和C欄的計算之差別,只是單筆的期數多了一期而已,其他則沒有什麼不同。
年金之現值
年金現值的計算也是將年金每期之金額一一以單筆折現回來,然後再計算其加總。Excel檔案裡,E、F兩欄是『現值』的計算,E欄是期末,F欄是期初。下圖是期末型態的年金,所以只要看E欄就可以了。E13~E18就是計算B13~B18每一『單筆』的現值,用的都只有公式(2)。例如E13是計算B13的未來值、E14是計算B14的未來值,依此類推。儲存格E12就是年金的終值:也就是E13~E18的加總。
等比年金試算
前面所述都是非固定比例之年金終值及現值的計算,可以看出只要將每期之現金流量一個一個列出來,就可以立即分別算出期初型態以及期末型態的年金終值與現值。既然每期不同數值都可以算了,每期『相同』或每期『等比例成長』之金額就更容易計算。
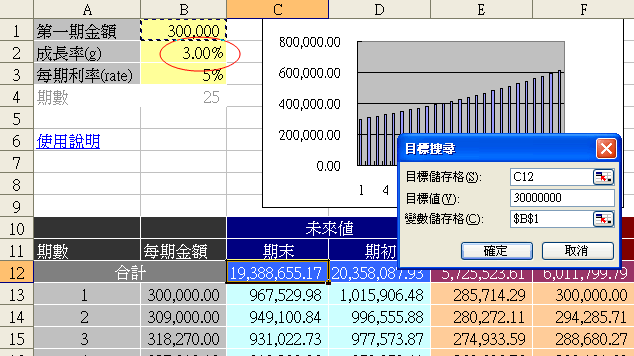
等比年金之每期金額(儲存格B13~B18),不需要一個一個手動輸入,如下圖所示只需要輸入每期金額(儲存格B1)及成長率(儲存格B2),然後會自動計算B13~B18的值,其他和非等比例變額年金完全相同。當成長率為0%時,也就是每期金額都一樣,相當於定額年金。
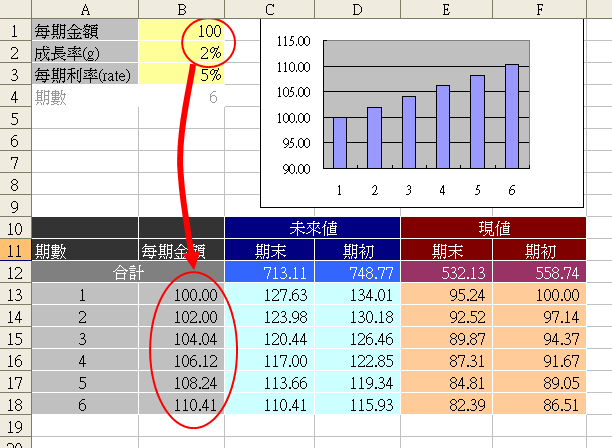
期末及期初之關係
不論是年金現值或終值,『期初年金』等於『期末年金』之(1+rate)倍。例如上圖期末型態的年金終值(儲存格C12)等於713.11,每期利率5%,那麼期初型態的年金終值=713.11*(1+5%) = 748.77。現值部份也是一樣,=532.13*(1+5%) = 558.74。
所以知道期末年金終值時,只要乘上(1+rate)就可立即算出期初年金終值。同理~~~知道期末年金現值時,只要乘上(1+rate)就可立即算出期初年金現值
期數的增減
雖然目前的工作表年金期數只有6期,不過這Excel的公式設計的讓使用者很容易增減期數。
增加期數
1) 在第1~6期中間插入欲增加之列數
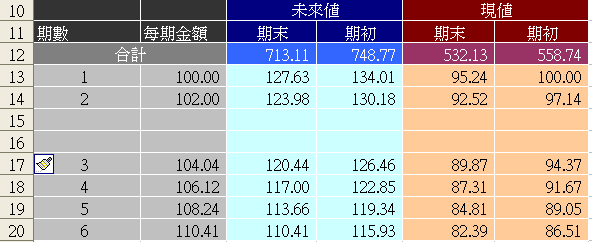
2) 點選第2期(下圖儲存格A14~F14),然後將將滑鼠移到儲存格F14的右下邊黑色小方塊,待+號出現後,按左鍵下拉至最後一期。也就是將第2期公式複製到其他的期數,這樣就大功告成,其他都不必改變。最後檢查一下C12的公式範圍是否由第一期加總至最後一期,如果是就沒錯了。
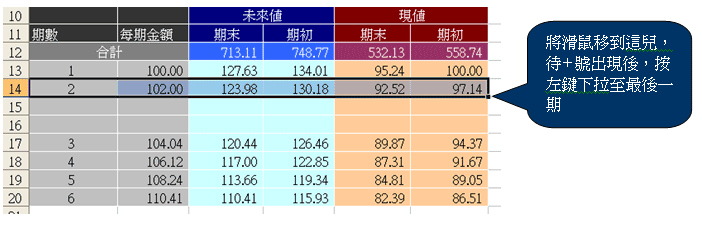
減少期數
減少期數就更簡單了,只要將多餘的期數整列刪除掉就可以了,但必須要注意從最後一期往前刪除。
如果讀者要增加期數的話,只需將最後一列複製起來,然後貼上所要增加的期數即可,其他公式都不必改變。只是圖表的部份需要手動改變範圍。
年金的應用
因為篇幅實在過大,有關使用年金的應用另外以一篇文章來呈現:年金(Annuity)-應用篇,裡面利用本篇的所製作的Excel來解任何複雜的年金問題,讓應用變得很簡單清楚。點選下圖也可以連結該網頁。
結論
透過Excel的年金現值及終值計算的分解動作,除了可以清楚了解年金終值的意義外,還可以將很複雜的變額年金變得非常簡單處理。管他的什麼年金公式,還用到等比級數來計算公式,全部把它丟到腦後!
延續閱讀
年金(Annuity)-應用篇
複利-完全攻略篇
Excel函數-FV未來值
附註:
定額年金的公式:
pmt:每期金額;rate:每期利率;nper:期數
年金終值公式(期末):
![]()

年金終值公式(期初):
![]()
年金現值公式(期末):
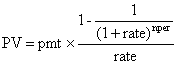
年金現值公式(期初):