如何算出最佳股債比例?
日期:2018-02-01
股債配置最佳的比例,幾乎是每一個投資者都想知道。因為股債的波動具有某種程度負相關,兩者相互配起來,就可以自動減低波動程度,所以公認是最佳的資產組合。至於股債比例應該多少,就得借助現代投資理論來求得答案。
資產組合理論主要用於分析不同資產組合在一起時,平均報酬率及波動風險會有甚麼樣的變化。波動風險是衡量報酬率偏離平均值的程度,一般使用統計學的標準差為標準。只要知道標準差就可以預估未來的報酬率,可能偏移平均值多遠。在自然分配情況下,有68%的機會偏離平均值一個標準差的範圍,95%的機會偏離兩個標準差。例如一檔股票基金平均報酬率10%,標準差15%,雖然未來實際發生的報酬率無法確定,但可預期68%的機會落在-5%~25%之內,有95%機會落在-20%~40%之間。
兩項 資產組合後的平均報酬率比較簡單(公式一),就是個別資產平均報酬率的加權平均,μ1、μ2是各別資產的平均報酬率,而兩項資產的權重分別為w1及(1-w1)。組合後的波動風險就比較複雜,除了個別資產的標準差σ1、σ2之外,還跟資產之間的相關係數η有關。兩種資產組合後的標準差σp如公式二。
μp= w1μ1+ (1-w1)μ2 … 公式一
σp2 = (w1σ1)2 + ((1-w1)σ2)2 + 2w1(1-w1)ησ1σ2 …公式二
其中w1、σ1是第一個資產權重及標準差,(1-w1)、σ2是第二個資產權重及標準差,η是最關鍵的相關係數,落在-1至+1之間的數值,當η為負值時,從公式二可以看出整體的波動度會減低。有了基本知識之後,就可以探討不同資產組合後的平均報酬率及標準差。
用實際的例子來說明就更清楚,先從最簡單的定存及股票的組合開始,股票選用追蹤S&P500指數的ETF,美國股票代號IVV。定存部位的比重w1,IVV的部位比重(1-w1),平均報酬率定存只有1% (μ1)、標準差0%(σ1)。因為定存報酬率不會波動,標準差等於0,公式二用σ1=0代入,就簡化成σp=(1-w1)σ2 ,也就是資產的標準差只剩IVV的標準差(σ2)乘上所持有的權重(1-w1)。
圖一:定存及IVV組合
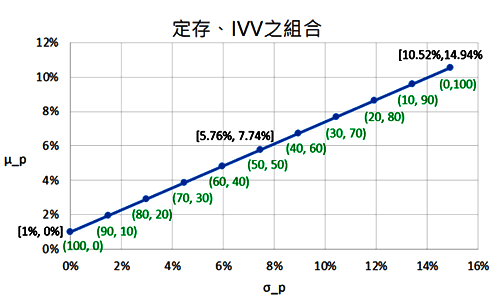
從Yahoo財經網站下載了IVV這檔ETF的歷史資料,以每一個月初的收盤價計算,獲得平均年報酬率10.52%(μb)及年標準差14.94%(σb)。有了這資料就可以根據不同權重下,可以獲得的平均報酬率以及標準差。如圖一所示,綠色括弧數字為部位比重,左邊為定存部位百分比,右邊為IVV部位百分比,可以看出隨著定存的比重增加,標準差就開始降低,同時報酬率也向定存1%靠攏,而且風險與報酬呈現線性關係。也可以這麼說,任何資產跟定存相配,風險與報酬都會呈現線性關係。這意思是說,如果希望波動風險比IVV還要小的資產組合,只要拿定存跟IVV配置,根據不同比例可以得到任意的平均報酬率及標準差。
上述的定存、IVV組合稍微改變一下,將定存的部位換成另一檔追蹤美國20年公債的ETF (TLT),兩檔的平均報酬率及標準差如下表,組合中沒有定存,都是股票及公債ETF,所以報酬率都會在平均報酬率上下變動,導致這兩檔ETF的標準差都不為0。又因為這兩檔ETF的相關係數-0.324,具有某種程度的負相關,配置後的結果會跟定存及IVV的組合有很大不同。
| ETF美股代號 | TLT |
IVV |
|---|---|---|
| 平均報酬率(μ) | 6.96% | 10.52% |
| 標準差(σ) | 14.39% | 14.94% |
| 相關係數(η) | -0.324 | |
IVV因為追蹤股票指數,平均報酬率只比TLT略高一點點,但是兩檔的標準差卻相差不多。如果只看報酬率及標準差,直覺上應該全部都持有IVV,因為兩者標準差幾乎相同,而IVV卻擁有較高的平均報酬率。然而,TLT真的毫無用處嗎,看看組合出來的平均報酬及標準差就知道了。
圖二的表格是不同比重的平均報酬及標準差,右邊是該表格以圖形呈現,括弧內綠色數字一樣是比重,左邊TLT右邊IVV。從上面最右邊的點開始看,全部IVV沒有TLT,這時候因為全部都是IVV所以平均報酬率及標準差都最高,隨著TLT的比重增加,雖然平均報酬率略為下降,但是標準差卻大幅的減少,到了兩檔各半的時候,落在組合的標準差最低點8.53%,而平均報酬率還有8.74%。
圖二:TLT、IVV之組合
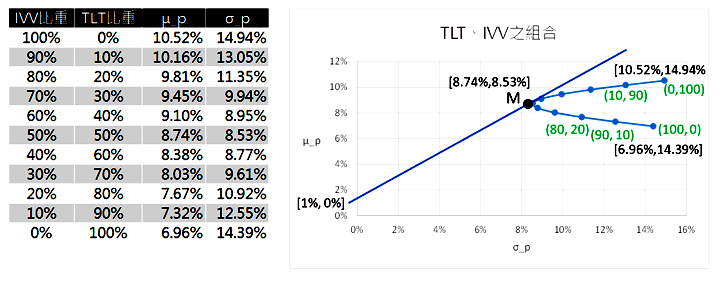
當TLT超過50%之後,平均報酬率愈來愈小,標準差卻又開始變大,最後百分之百TLT的時候,平均報酬率只有6.96%,而標準差等於TLT的14.39%。理性的投資者只會選擇IVV50%~100%之間的比重,不會選擇IVV比重小於50%的組合,因為平均報酬率變少,而標準差卻變大了。
比較定存、IVV (A組合)以及TLT、IVV(B組合),B組顯然比A組還要好。若要將A組的標準差降到B組的最低點8.53%,IVV的持有比重必須是57.1%(=8.53/14.94),那麼A組合的平均報酬率只剩6.4%,而B組合平均報酬率卻可以獲得較高8.74%,標準差數值都一樣是8.53%,B組的平均報酬率可以高於A組。也可以說B組只犧牲一點的報酬率,便可以換得較低的波動度。會有這種現象是兩檔ETF相關係數η-0.324,而組合中的TLT是配角,主要用來降低風險(標準差)。
可是IVV、TLT再怎麼配,標準差最低也是8.53%,對於風險承受度較低的投資者,可以透過定存及B組的資產配置,就可以組出任意標準差的組合,至於B組資產IVV、TLT該多少,可以在垂直軸選擇定存1%,畫出和B組資產組合線的相切的直線,切點就是最佳組合。從圖中M點就是該組合,用肉眼看IVV、TLT各半。
圖三是定存與M組合在不同定存比例下的結果,定存比例愈高標準差愈小,同樣的報酬率也愈少。投資時先選定自己可以承受的風險,也就是標準差,再從圖三的表格找出定存的比重,其他的就投資M組合。
圖三:定存與M之組合
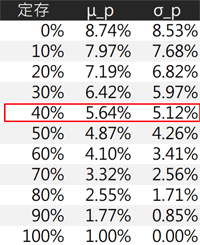
例如Peter用圖三覺得40%的定存,可以獲得5.64%的平均報酬率及5.12%標準差,這樣的組合最適合自己。若預計投入100萬元,那麼40萬應該投入定存,剩下的60萬投入M組合,也就是TLT及IVV各半,TLT及IVV各30萬元。對於這樣的投資組合,Peter可以預期每年的投資報酬率,會有68%機率會落在平均值上下一個標準差之內(0.52%~10.76%),有95%機率會落在平均值上下兩個標準差之內(-4.59%~15.88%)。也就是說這樣的組合只有0.25%的機會虧損超過負4.59%。
透過以上的分析,相信對於股債的比例會有新的認知,對於資產的布局也才更有信心。
後記:TLT跟〈元大美國政府20年期(以上)債券基金〉之ETF(股票代號 00679B)所追蹤的指數是一樣的,而IVV跟〈元大標普500基金〉之ETF(股票代號 00646)所追蹤的指數都一樣,差別就是元大投信基金的費用率較高。所以國內的投資者持有00679B及00646,也相當於持有TLT及IVV。







