定期定值之理論基礎
日期:2010-02-15
因應定期定額投資的種種問題,哈佛金融學院教授Michael E. Edleson,於1988年寫了一篇文章「Value Averaging: A New Approach To Accumulation」,介紹一種改良式的定期定額投資策略,有效的解決定期定額鈍化的問題,以及提升整體之投資報酬率。台灣翻譯成定期定值投資策略,其實我倒是認為這是一種「目標追蹤法」。這種方式有兩個特點:
- 預期投資金額會隨著時間而成長
- 每期金額會依目前績效偏離目標之程度而動態調整
貨幣時間價值
定期定值特點之一是考慮貨幣的時間價值,也就是今天1元的價值和5年、10年後是不一樣的,那麼每期投入的金額也應該「價值」一樣才是,也就是說每期投資金額至少要隨著通貨膨漲率而提高。而且隨著時間拉長,累積的投入單位也愈來愈多,如果投入金額沒有增加,每期投資之金額佔本金的比例會愈少,就會發生和定期定額一樣的鈍化現象。為了強化每期投入對本金的影響力,定期定值使用成長率"g"的觀念,基本假設是每期投入金額,均為上一期的(1+g)倍:
每期投入之金額 = 上一期投入金額*(1+g)
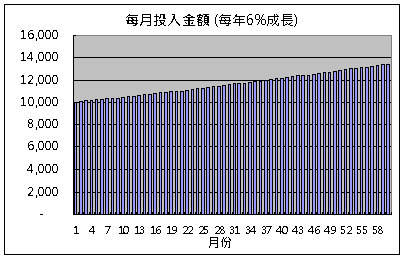
▼第一次投入1萬元,每年以6%成長
期末終值計算公式
假若投資報酬率為"r",每期之投入金額成長率為"g",第一期「初」投入金額為C,那麼到了"n"期末投資結束時之終值(FV)如下面公式(一)所示,這也就是投資所要達到之最終目標值。
▼公式(一)
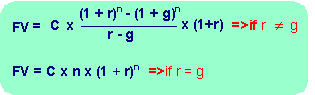
反過來當目標值(FV)為已知時,當然可以用公式一求出第一期投入金額"C"了。公式(一)是成長型之年金終值計算公式,公式(一)有兩項,分別適用"r"以及"g"相等以及不相等的情況。另一個約估的方式(公式二),適用任何"r"與"g,雖然是大約之公式,但實用上準確度也相當足夠了。
▼公式(二)
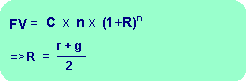
例如希望10年後可以有500萬存款,預期年報酬率12%,每年投入金額成長率為6%,每「月」為一期,那麼第一月投入金額( C ):
月報酬率:1% (=12%/12)
月投入金額成長率:0.5% (=6%/12)
平均(R):0.75% [=(1%+0.5%)/2]
期數(n=120)
所以第一月金額( C ):
公式一(精算)
=(5000000*(1%-0.5%))/((1+1%)*((1+1%)^120-(1+0.5%)^120))
=16,714
公式二(概算)
= 5000000/(120*(1+0.75%)^120)
= 16,997
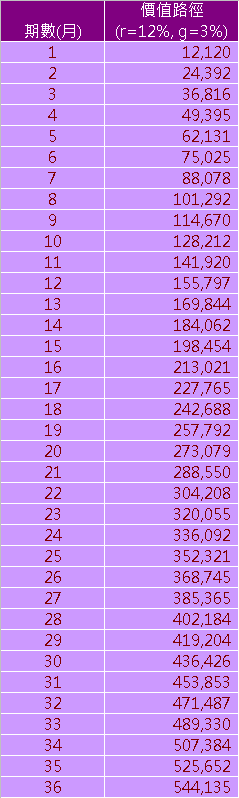
價值路徑
當每一期所投入的金額均以g成長率增加,也就是每一期均為上一期之(1+g)倍,而且所有已投入資產,每期皆會以"r"的報酬率成長,那麼經過n期後,累積的每期之期末價值所畫出來的軌跡就是價值路徑,也就是預期的資產成長軌跡。
▼投入金額年成長率3%、年報酬率12%,第一期投入12,000之價值路徑圖
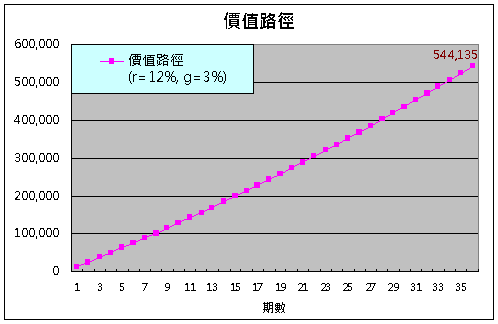
上圖之價值路徑可以運用根據公式一,很容易的做出來,如下表所示:
多退少補策略
價值路徑是根據投資規劃所做出來的,可是實際投資報酬可不會死板板的如預期般發生,定期定值的策略是:每一期均檢視過去累計單位數之總淨值,離當期的價值路徑多遠,若比當期價值路徑少,就將缺額補足;若已投資的淨值已經高於預期,就賣出手中持股。這樣的機制當股市上漲幅度高於預期報酬率時,就會買得愈少;股市下跌時,就會買得比預期多,使得手中持股僅貼著價值路徑走。
例如一投資計畫從2007年2月起,希望3年後目標54萬元,期望報酬率12%,投入金額年成長率3%,所以投資路徑跟上表一樣。台灣50ETF,2007年2月淨值為NT$56.66,所以第一期買入單位數為213.9075(=12120/56.66)。到了3月時淨值降為NT$55.94,價值路徑第二期要求淨值24,392,所以缺額為:
=24392-213.9075*55.94 = 12,426
第二期買入單位數:
=12426/55.94
=222.1309
累計單位數=222.1309 + 213.907 = 436.0379
依此類推,每一期都依當期預計之價值路徑扣除所持有累積單位數之總淨值,正值就是要加購之金額,負值就是賣出之金額,使得所有持股價值緊盯價值路徑走。
定期定值試算
在「定期定值投資策略」一文裡,有回流測試之試算,讀者可以看看試算出來之結果,還有提供投資明細,是個有效的分析工具。
參考資料
定期定值試算
年金-理論篇
年金-應用篇
定期定值投資策略書籍(寰宇出版)
A
STATISTICAL COMPARISON OF VALUE - AVERAGING VS. DOLLAR COST AVERAGING AND
RANDOM INVESTMENT TECHNIQUES






