如何用科學方法做投資決策?
日期:2021-04-09
我們都知道投資個股的風險比較大,投資定存的風險比較小,然而光靠這樣的描述是沒辦法做投資決策的,必須知道投資某項資產,獲利的機率有多少,以及虧損的機率又有多少,這樣做決策才容易。
這就好似氣象預報,每次颱風一來,市長在前一晚就得做出決定是否放颱風假,然而只有天知道隔日會不會出現七級陣風,但是氣象局若能預估出現的機率對決策就很有幫助了。投資也是一樣,若能預知獲利及虧損的機率,就可以比較正確的做好投資決策。
報酬與風險是一體兩面,缺一就無法正確描述。報酬就是以報酬率表示,而風險是以標準差表示。報酬率也有累積報酬率、年化報酬率以及平均報酬率之分,所代表的意義都不一樣。投資者通常較關心投資績效,看的都是累積報酬率及年化報酬率。然而,這些都是過去績效,對預估未來沒有幫助,只有平均報酬率才是預估用的。
首先就得先了解報酬率的意義,公式是獲利(虧損)除上投入金額(如圖一),獲利就是期末比期初投入多出來的部分,虧損就是期末比期初投入少掉的部分,也就是比原來投入金額多了多少,或是少了多少,所以報酬率其實是成長率的概念,也就是資金的成長率,是衡量投資最重要的關鍵因素。
圖一:投資報酬率就是資金成長率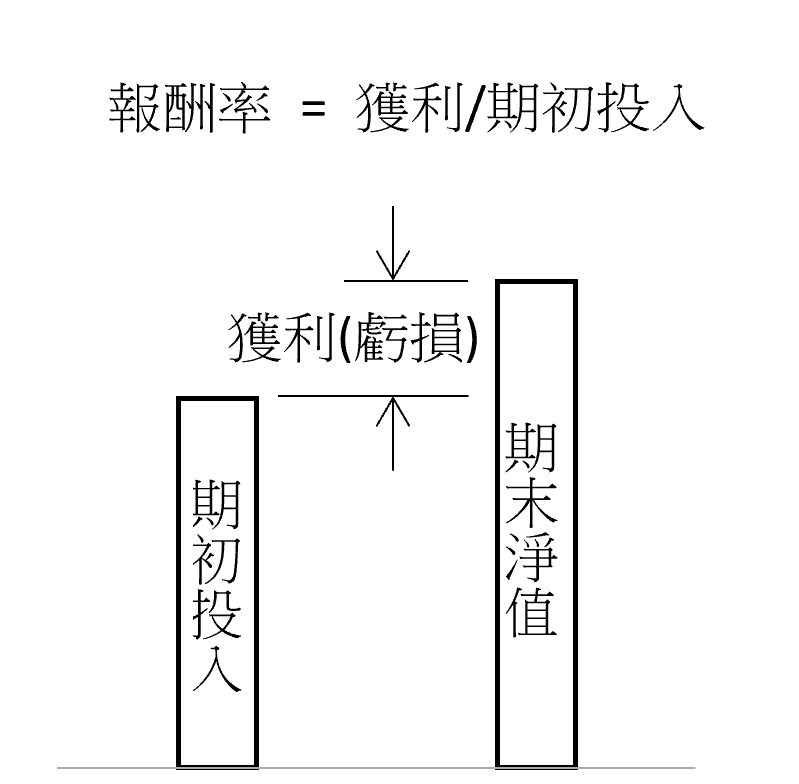
一般的報酬率若沒有特別指明,就是一段期間的累計報酬率,例如股票代號0050這檔元大發行ETF,2018/2/5收盤價83.6元,到了2021/2/5收盤價134.8元,價差51.2元,加上這期間配息共10.35元,價差加上配息總共61.55元,除上期初收盤價,報酬率為73.6%,也就是獲利是投入金額的73.6%,也可以說投入金額成長了73.6%。
然而這是未考慮配息再投入的結果,如果期中領到的配息當天再投入的話,最後結果就不一樣了,而且時間愈久就差愈多。表一假設在2018/2/5以83.6元買進0050一張,投入金額8萬3,600元,擁有股數1,000股,到了2018/7/23收到每單位配息0.7元,配息收入共700元,當日收盤價84.55元,可以買到8.28股,累積股數1008.28股。到了第2次配息時,每單位配息2.3元,收到的配息就不再是乘上1,000股,而是乘上累積股數1,008.28股,總共收到配息2,319元,當天收盤價74.05元,可以買到31.32股,累積單位數來到了1,039.6股。依此類推,到了最近的配息日2021/1/22,累計單位數來到了1,114.03單位,在期末2021/2/5之前都沒有再配息,所以維持單位數1,114.03,該日收盤價134.8元,總淨值為15萬170元,累積報酬率79.6%【=150170/83600-1】。通常將配息再投入的報酬率稱之為投資績效。
表1:0050最近3年配息
| 除息 | 每單配息 | 收盤價 | 配息金額 | 股數 |
|---|---|---|---|---|
| 1,000.00 | ||||
| 2018/7/23 | 0.7 | 84.55 | 700 | 1,008.28 |
| 2019/1/22 | 2.3 | 74.05 | 2,319 | 1,039.60 |
| 2019/7/19 | 0.7 | 83.00 | 728 | 1,048.37 |
| 2020/1/31 | 2.9 | 89.95 | 3,040 | 1,082.16 |
| 2020/7/21 | 0.7 | 98.70 | 758 | 1,089.84 |
| 2021/1/22 | 3.05 | 137.45 | 3,324 | 1,114.03 |
這是3年的投資累積績效,若是換算成每年的報酬率,又稱之為年化報酬率,計算方式得考慮複利,並不是單純的除上3,而是用下列Excel公式計算:
年化報酬率 = (1+累積報酬率)^(1/年數)-1
所以0050最近3年的累積報酬率為79.6%,相當於年化報酬率21.6%【=(1+79.6%)^(1/3)-1】。
風險量化後才能預估未來報酬範圍
累積報酬率及年化報酬率是結果論,至於是如何得到這樣的累積報酬率,過程又是如何,當中承受了多少風險,並沒有提供這樣的訊息。現代投資組合理論使用報酬率的平均值與標準差,就可以預估未來報酬率的機率分布,提供投資決策的依據。
方法是蒐集一組資產固定期間的每一期報酬率,然後算出平均值及標準差。平均值就是所有報酬率的算術平均,而標準差則是報酬率偏離平均值的程度。標準差愈大並不代表全然不好,如果報酬率比平均值高出許多,這是好現象,但也代表穩定度不夠,會比平均值高出許多,也代表會比平均值低很多,只是機率各半。只要報酬率的平均值是正的,那麼淨值的長期趨勢就會往上走,而標準差愈大,淨值偏離平均值就愈多,可能比平均值高,也可能比平均值低,這就是波動風險愈大。
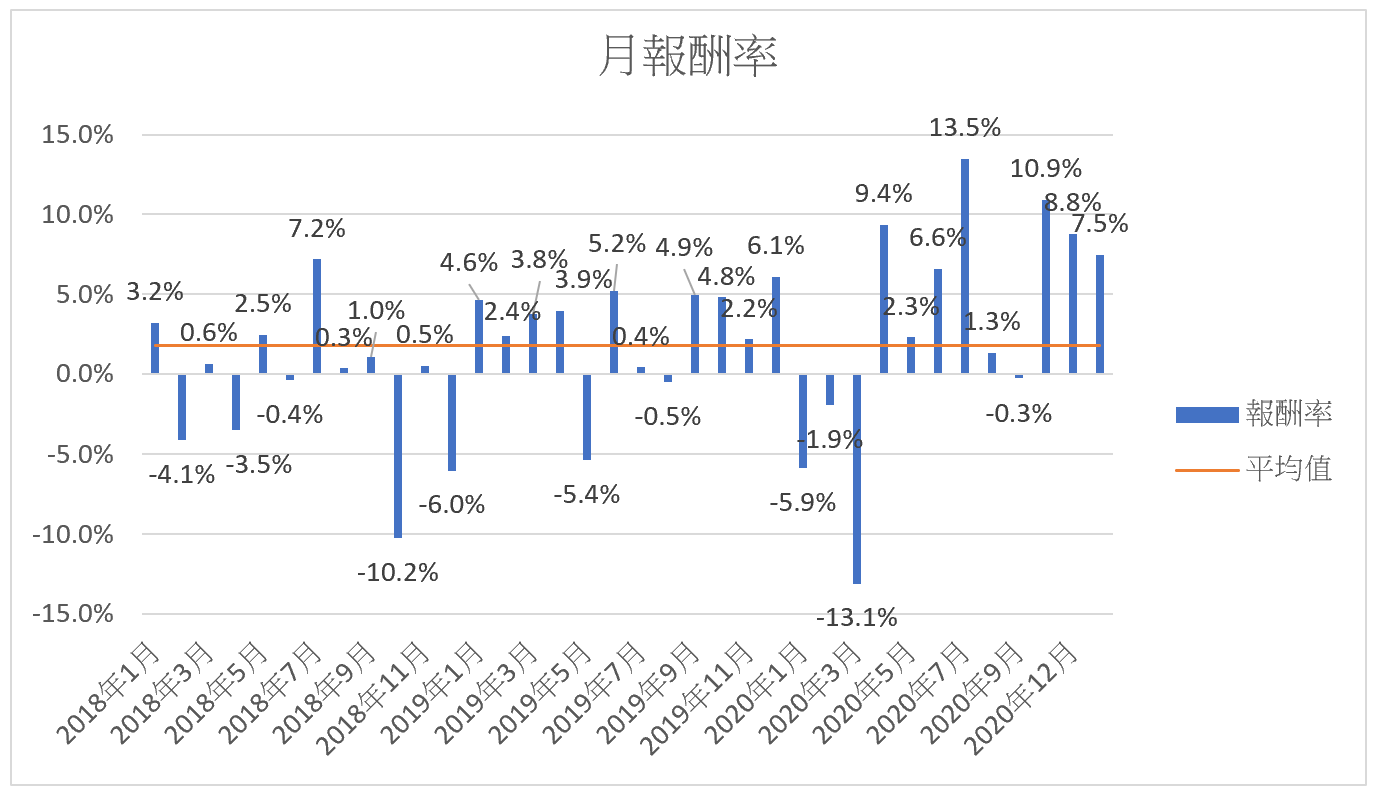
就以最近3年的0050績效為例,每個月都假設月初買入月底賣出,這樣可以求得36個月的報酬率,每月報酬率如圖2,這些報酬率的平均值為1.74%,標準差5.6%。平均值及標準差可以分別用Excel的AVERAGE及STDEV.S函數計算,只要將每月報酬率代入公式即可。
有了平均值及標準差,就可以預估未來落點的機率,只要是常態分配,68%的機率會出現在平均值正負一個標準差之內,就是平均值減掉1倍的標準差,以及平均值加上1倍的標準差,95%機率會出現在平均值正負2倍標準差之內,99.7%的機率會出現在平均值正負3倍標準差之內。
例如預估某家超商每天可以賣出多少個茶葉蛋,只要將過去一個月每日的銷售紀錄拿出來,求得平均值及標準差,就可以推估每一天銷售量的可能落點。例如過去3個月平均起來每日銷售400顆,標準差50顆,那麼每日有68%的機率銷售量介於350~450顆,只有13.5%機率會在300~350顆之間,也只有13.5%機率介於450~500顆,但是再少也不會少於250顆,再多也不會多於550顆。為何是這些數字,因為平均值400顆,標準差50顆,每偏離平均值一個標準差就是偏離50顆,所以是350, 300 , 250以及450, 500, 550顆茶葉蛋。
但是過去績效不代表未來,這是正確的。就好似今天賣了520顆茶葉蛋,並無法期待明天也可以賣520顆,但是過去茶葉蛋銷售的系統特性,是可以用過去資料預估的,而銷售數量的平均值及標準差,就是這家超商銷售茶葉蛋的系統特性。只要用過去1個月或3個月的銷售平均值及標準差,就可以當作超商的系統特性,用於評估未來落點,當中會有些許誤差,但是在可接受的範圍。
0050的系統特性在過去3年,每月報酬率的平均值為1.74%,標準差為5.6%,就可以用來預估未來一個月報酬率的範圍,就是有68%機率會落在平均報酬率正負一個標準差之內,在-3.9%~7.4%之間,只有13.5%機率月報酬率落會在-3.9%~-9.6%,也只有13.5%機率月報酬率會介於7.4%~13.0%。
上述情形是每月報酬率的狀況,那麼每一年報酬率及標準差會是多少?如果用過去每一年的報酬率來算平均值及標準差,會出現樣本數不足,過去10年也只有10個年報酬率可用,精確度就大打折扣。實務上都使用月報酬率及月標準差去推估年報酬率及年標準差。年平均報酬率等於月報酬率乘上12,年標準差等於月標準差乘上開根號12。0050過去3年月報酬率1.74%,月標準差5.6%,所以相當於每年平均報酬率為20.9%【=1.74%*12】,年標準差為19.6%【=5.6%*12^0.5】。簡單解讀為68%的機率,每年報酬率會出現在1.4%~40.5%之間,只有13.5%機率每年報酬率出現在-18.2%~1.4%之間,也只有13.5%每年報酬率出現在40.5%~60%之間。
有了這樣的數據,對標的的選擇及投資決策是不是就可靠許多了。
圖2:0050最近36個月的報酬率