債券資產遠比想像中更重要
日期:2021-01-05
債券資產在投資領域中的重要性,遠比想像中還更重要,並不只是債券的風險較小,而是資產加了債券以後,整體報酬率才有機會大於單獨持有股票。雖然債券在資產配置中不能算是主角,但卻是不可或缺的配角!
投資報酬率是用來量化一項投資資產最有效的工具,然而報酬率並不是固定一成不變,而是每天、每年都在變化,於是描述的方式除了使用平均報酬率之外,還多加了一項波動度,就是報酬率偏離平均值多遠,也就是統計上使用的標準差,標準差愈高,就代表偏離平均報酬率愈多。報酬率波動的程度又可以解釋為風險,所以投資所說的報酬與風險,指的就是平均報酬率與標準差。
例如00646這一檔追蹤S&P 500指數的ETF,過去3年的平均報酬率11.1%,標準差16.0%,另一檔00679B是追蹤ICE美國債券指數的ETF,過去3年的平均報酬為7.6%,標準差12.4%。要說這兩檔那一個比較好就很難分別,因為不能只看平均報酬率,還得看標準差,而每一個投資者承受的風險都不一樣。若是問哪一檔的性價比(CP值)比較高,那就容易了。只要算一下夏普值就知道了,因為其意義就是每承擔一單位的風險,可以獲得多少報酬,公式如下:
夏普值 = (平均報酬率 – 無風險利率) / 標準差
而無風險利率一般用定存利率替代。每一項個別資產擁有一個夏普值,不同資產互相搭配後又可以得到另一組夏普值,而資產配置的目的,就是找出最高夏普值的組合。資產配置跟資產之間的相關性有很大關聯,相關性愈低,能獲得的夏普值就愈高,尤其具有負相關的資產相互搭配,可以獲得的夏普值也愈高。00646及00679B過去3年的相關係數為-0.45,所以可以組出更高的夏普值。表一列出了不同組合的平均報酬率、標準差以及夏普值,00646的夏普值0.643,00679B的夏普值0.548,兩者搭配後的組合A的夏普值1.118。
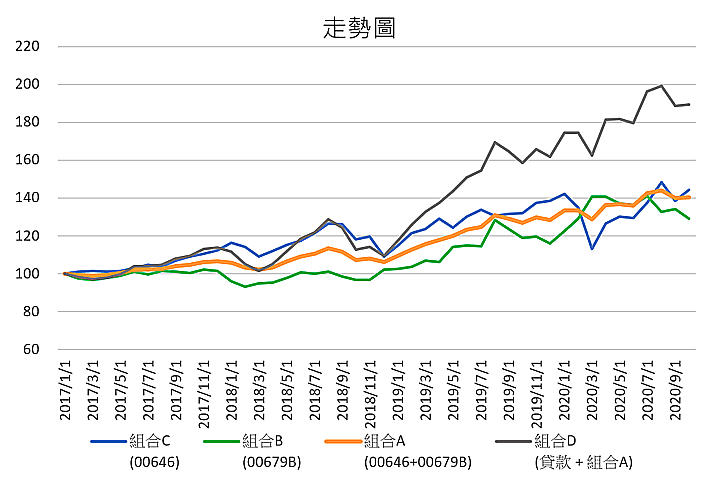
圖一的走勢圖,藍色線條為只有00646的走勢,綠色線條為只有00679B的走勢,而橙色線條則是組合A (50% 00646 + 50% 00679B),很明顯的可以看出組合A很平穩的往上走,最後的淨值只略少於00646。這就是夏普值的意義,同樣的報酬可以波動更小,或是同樣的波動可以獲得更高的報酬。而灰色線條則是組合D的走勢,比組合A略低的夏普值,只是透過財務槓桿,提高平均報酬,但是標準差跟只有00646一檔一樣都是16.0%。
或許有人會說自己還年輕,願意承擔較高的風險,想要較高的報酬,於是希望全部持有股票,不需要搭配債券。這是錯誤的觀念,因為較高夏普值的組合,只要再跟定存搭配,就可以獲得一個新組合,標準差跟股票一樣,但是平均報酬率會比較高。
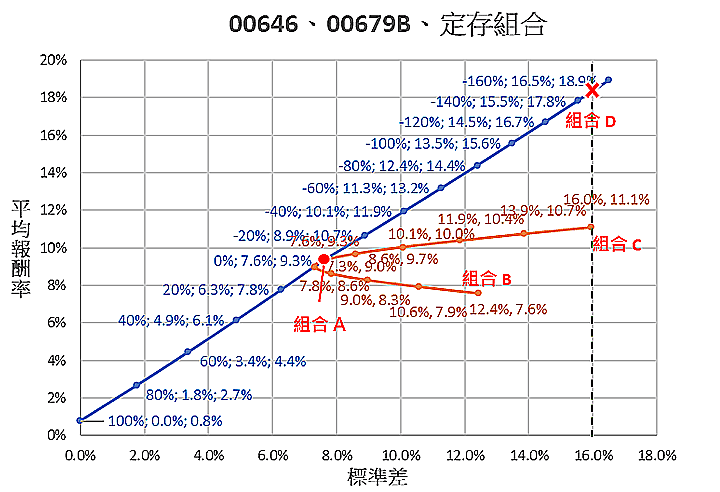
例如全部持有00646,平均報酬率11.1%,標準差16.0%。全部持有00679B平均報酬率7.6%,標準差12.4%,這兩項資產互相組合後就是圖二中的橙色曲線,搭配後的平均報酬率與標準差,又稱為組合之效率前緣。橙色線上每一個點差別只是部位比例不同,右上終點就是組合C,也是全部00646,沒有00679B。線條往左邊移動,每一點代表00646的比例降低10%,到了中間的紅點就是剛好50% 00646及50% 00679B,也就是組合A,接著往下反轉直到最後端點組合B,就是全部00679B,沒有00646。
另外還可以用定存與橙色線的任何一點再組合,因為定存標準差為0,所以組出來一定是直線。橙色線中夏普值最高就是組合A,所以圖二中的藍色直線就是以組合A的資產及定存的新組合,又稱為資金配置線,這一條線的斜率就是夏普值,因為定存與組合A的新組合,每一點的夏普值不變,都跟組合A的夏普值一樣。藍色線條在組合A以上部分,因為加了入貸款必須支付利息,所以夏普值會略低。
藍色線上每一點代表不同定存所占總資產的比例,例如定存占總資產30%,組合A占70%,所以00646及00679B各占35%,加總100%。若是定存占總資產50%,那麼00646及00679B就各占25%,加總也是100%。每個藍色點上的3個數字,最左邊代表定存占資產比例,中間的數字為組合後之標準差,最右邊數字為平均報酬率。
圖二藍色直線最下方的點就全部是定存,組合A比例為0,往右上走定存比率愈低,與橙色線相交的點也是組合A,這一點定存占總資產比例為0,所以全部都是組合A,這點平均報酬率9.3%及標準差7.6%。藍色線穿過組合A這點再往右上走,定存比例開始變成負值,代表不只沒有定存,反而是貸款來投資組合A。可以看到隨著貸款比例增加,平均報酬率及標準差也隨著增加,這就是財務槓桿,會放大報酬也會放大風險。
藍色線再往上走會跟一條綠色垂直虛線相交,這一點稱為組合D,定存比率為-150%,標準差16.0%,平均報酬率18%。這一點的標準差跟組合C(全部00646)一樣都是16.0%,但是平均報酬率卻是18%。定存比例-150%是說,原本投資金額100萬元,再借150萬元,總投入250萬元,但是150萬元得支付利息。
簡單說,若要全部持有股票(組合C),還不如持有組合D,因為這兩項資產的標準差一樣,可是組合D的報酬率卻是高出很多。圖一中的灰色線條,就是組合D的走勢圖,很明顯的高於全部00646的藍色線,而這兩條線的波動程度(標準差)是一樣的。若沒有00679B這項債券ETF,就沒有藍色這條線,就不會出現組合D的選項,這才是債券資產最重要的貢獻。
單獨持有債券型基金或ETF,報酬率確實不是很吸引人,但就因為股債之間具有負相關,組合起來才會讓波動大幅降低,再透過定存更能組出具任何波動風險的組合,這就是債券型基金或ETF為何那麼重要的原因,因為沒有債券資產就不會有藍色那條資金配置線。看完這篇,你還敢說債券是保守投資者的專利嗎!
表一:00646與00679B之平均報酬與標準差
| 證券代號 | 平均報酬率 | 標準差 | 夏普值 |
|---|---|---|---|
| 00646(組合C) | 11.1% | 16.0% | 0.643 |
| 00679B(組合B) | 7.6% | 12.4% | 0.548 |
| 組合A (50% 00646 + 50% 00679B) | 9.3% | 7.6% | 1.118 |
| 組合D (貸款150% + 50% 00646 + 50% 00679B) | 18.4% | 16.0% | 1.02 |
圖一:00646、00679B、各半的組合及加上150%貸款
圖二:各組合及效率前緣